Implementing a Biquad Cascade IIR Filter on an ARM Cortex M4 using CMSIS DSP
The use of FIR vs. IIR filters is discussed elsewhere at length:
-
Pitfalls of Filtering the EEG Signal by Sapiens Lab
-
Difference between IIR and FIR filters: a practical design guide by Advanced Solutions Nederland
For fast, lightweight computation—most applicable to closed-loop applications—the IIR is ideal (see also, A Fast EEG Forecasting Algorithm for Phase-Locked Transcranial Electrical Stimulation of the Human Brain). Using the CMSIS DSP library is probably the fastest way to implement such a filter on equipped ARM hardware. The key to implementing the filter is generating the filter coefficients which end up being part of the arm_biquad_cascade_df2T_instance_f32 struct.
Matteo posted a great toolset for GNU Octave which I ported to MATLAB. However, the lines of code to get the coefficients is rather simple and straight forward. It comes down to the second-order section (SOS) digital filter, specified as an L-by-6 matrix, where L is the number of second-order sections (see sosfilt() in MATLAB).

Second-order section filter matrix.
In this example, I generate a low-pass elliptical filter. This code can be generated by the Filter Design Tool in MATLAB.
Hd.sosMatrix contains the SOS matrix. You can derive the SOS matrix in other ways, like using ellip() followed by zp2sos(). To use the coefficients with an ARM device, the fourth column is removed, the last two columns undergo a sign reversal, and the matrix is flattened.
Implementing on ARM
There is a CMSIS example of using an FIR filter which I have used as a model (caveats discussed below). I have combined the boilerplate from Matteo with this example for my final implementation; note that this initializes the filter instance manually (without the init function), but shows how to filter the signal in blocks, like the example. The input signal is found in SWAsignal.h.
I suspect that the example uses a for-loop, block-filtering approach because it is adaptable to larger input signal buffers and can be optimized for a particular architecture. However, I found that a 1,024 point buffer has an 80 microsecond advantage from being run in one line while eliminating a lot of code complexity.
arm_biquad_cascade_df2T_f32(&filtInst, inputSignal, filtSignal, SIG_SAMPLES);
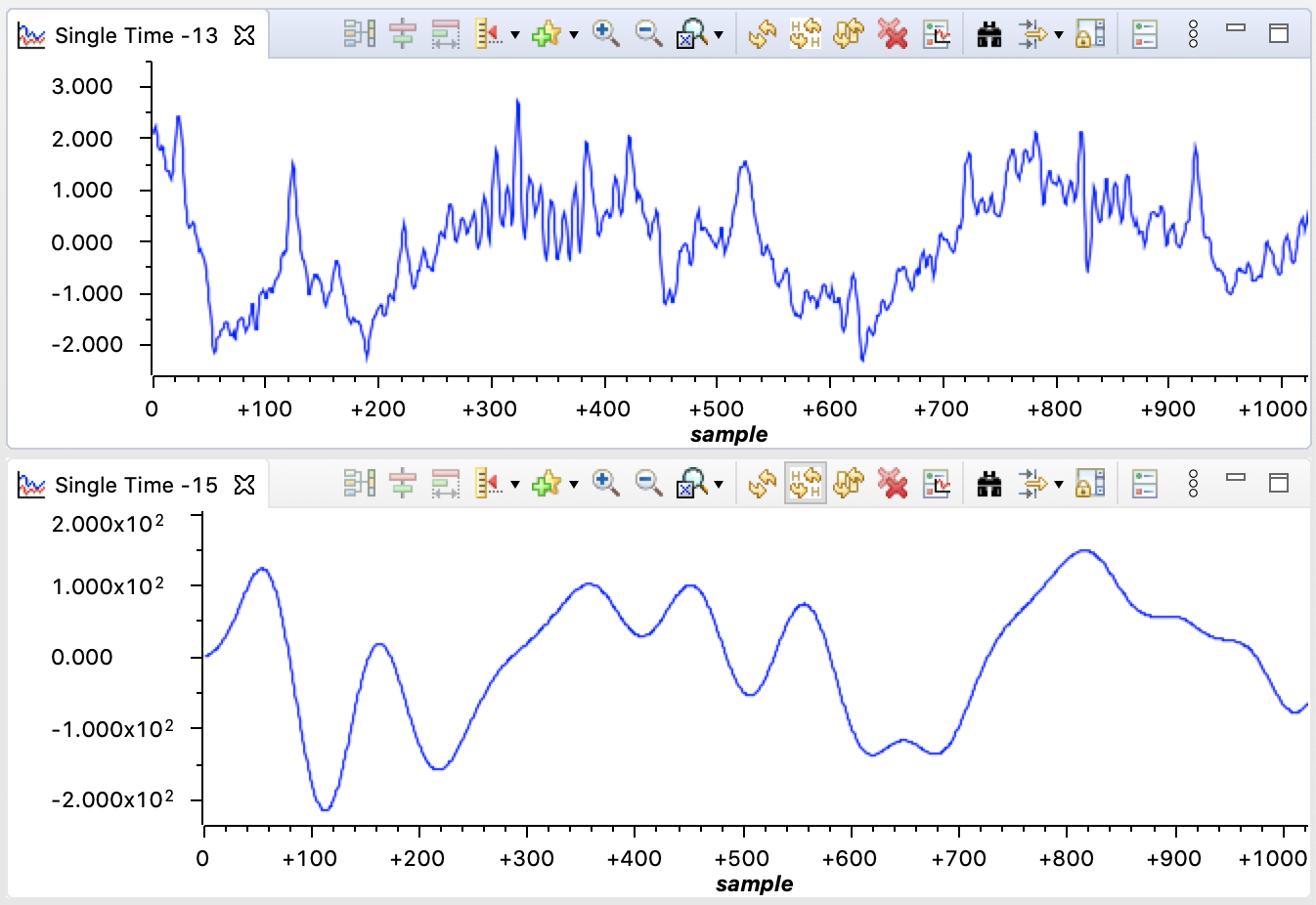
Top: unfiltered signal, Bottom: low-pass filtered signal
Recent Comments
Archives
- April 2023
- January 2023
- November 2022
- May 2022
- March 2022
- January 2022
- December 2021
- April 2021
- December 2020
- October 2020
- August 2020
- July 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- January 2019
- December 2018
- November 2018
- August 2018
- July 2018
- April 2018
- March 2018
- November 2017
- October 2017
- February 2017
- October 2016
- August 2016
- July 2016
- November 2015
- October 2013
- February 2013
- January 2013
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- February 2012
- December 2011
