Equalizing Sampling Rate for 1-D Correlations in MATLAB
We often have two signals with different sampling rates that we want to correlate. One example is when we want to correlate local field potential (LFP) activity of a neural signal to some average spike rate of a neuron. Our LFP signal is recorded at 24 kHz, but the spike density estimate (SDE) we create from individual spike timestamps is given an artificial sampling rate of 1 kHz. End-to-end, the LFP and SDE are potentially correlated, but to operate on those as variables in MATLAB they need to be the same length.
In this function, we use 1-D interpolation to force d1 data into the length of d2 and call that d1new. Ideally, your d2 data has the higher sampling rate so that d1 is being ‘upsampled’ instead of ‘downsampled’.
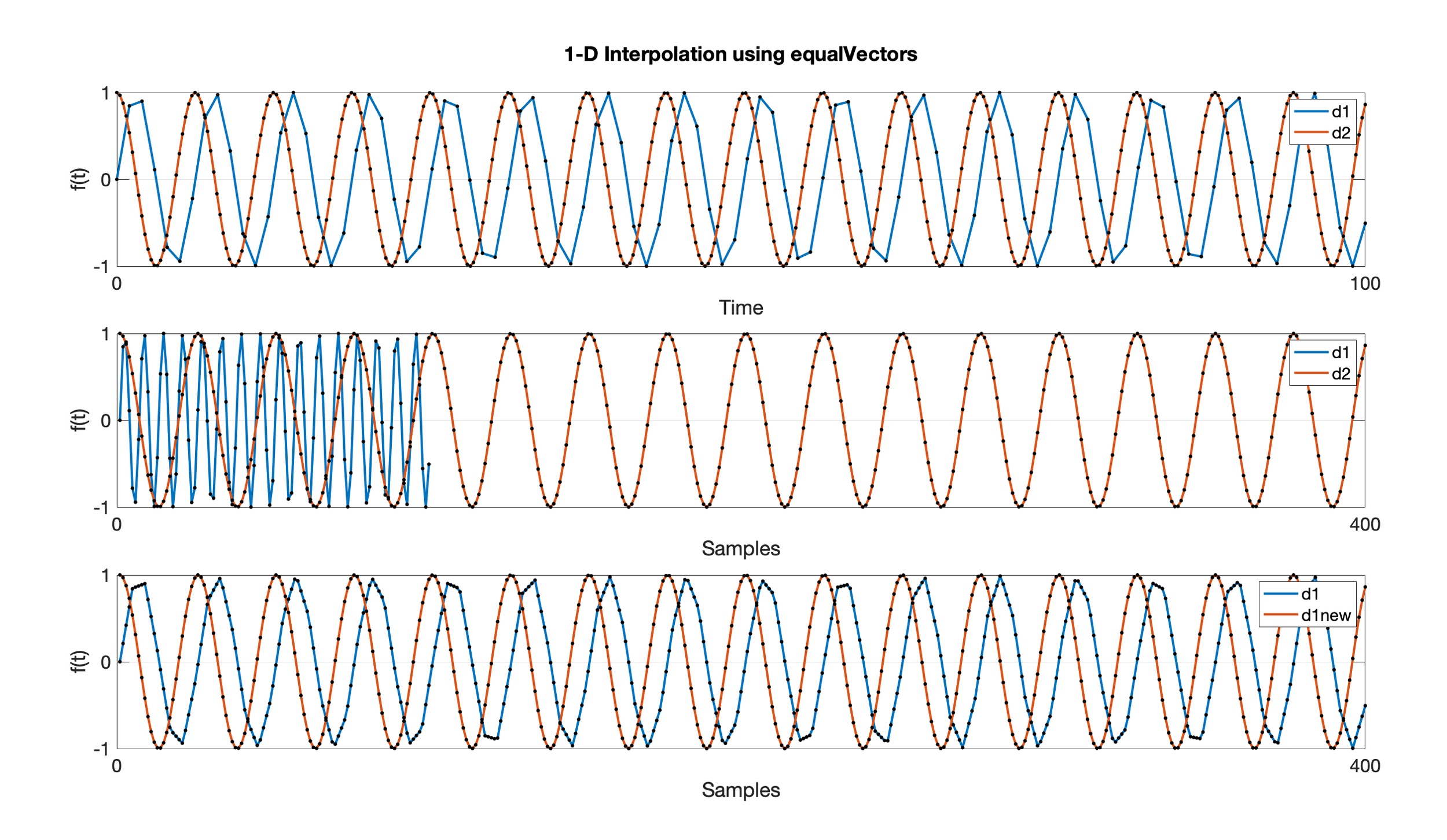
Consider two signals (d1 and d2) where f is either sin() or cos() and the time variable t is 0-100s, but each t has a different sampling rate.
t1 = linspace(0,100,100); % 0-100s, 100 points, 'low' sampling ratet2 = linspace(0,100,400); % 0-100s, 400 points, 'high' sampling rated1 = sin(t1);d2 = cos(t2);d1new = equalVectors(d1,d2);The top plot shows the signals overlaid in Time with each point from t marked in black. The middle plot highlights that when plotted by Samples, the two signals are unequal in size. The bottom plot shows how 1-D interpolation through equalVectors and the d1new variable equalize the vector lengths, thereby making a correlation possible.
Recent Comments
Archives
- April 2023
- January 2023
- November 2022
- May 2022
- March 2022
- January 2022
- December 2021
- April 2021
- December 2020
- October 2020
- August 2020
- July 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- January 2019
- December 2018
- November 2018
- August 2018
- July 2018
- April 2018
- March 2018
- November 2017
- October 2017
- February 2017
- October 2016
- August 2016
- July 2016
- November 2015
- October 2013
- February 2013
- January 2013
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- February 2012
- December 2011
